Create Date: July 13, 2024
Last Modified Date: December 10, 2024
Calculating constant of proportionality can be done with the following formula:
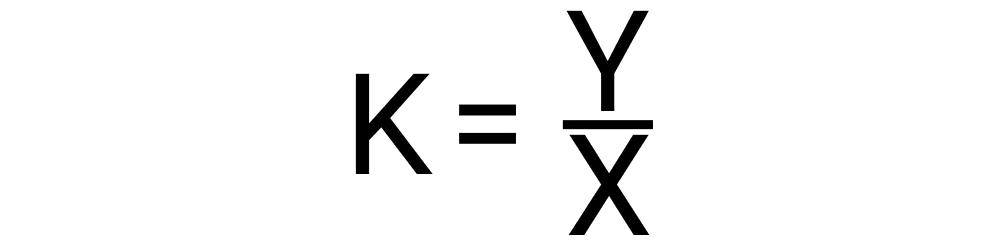
The result you get from this tool will be a single number. This number may not be a whole number. The result identifies what the dependent variable is in terms of the independent variable. If the result is .5 that means the independent variable you entered is double the dependent variable.
Using a tool to calculate constant of proportionality can save you a headache as well as time. The steps involved with using our tool to find this value include:
Imagine you have a job where what you earn depends directly on how many hours you work. In this situation, “time worked” and “money earned” have a direct proportional relationship. If we say the constant of proportionality is 1.4, it means that for every hour you work, you earn 1.4 dollars.
No matter how many hours you put in, your earnings always remain 1.4 times the number of hours worked. This “1.4” is the constant of proportionality—it’s the steady factor that links your time worked (x) directly to the amount you earn (y).
It’s often seen in scenarios like unit conversions, rates of growth or change, and scaling models or recipes. The constant of proportionality represents the consistent relationship between variables in these cases.
Yes, they are closely related. The constant of proportionality can be thought of as the rate or slope in a linear relationship, as seen in equations like y = mx, where m is the slope or constant of proportionality.
Calculate the similarity between the data you got and the expected distribution with chi-square.
Calculate the percent chance of a number of different outcomes for three events occurring.
Calculate the relative error between a measured value and the actual value.
