Combination Calculator

Knowing how many combinations you can make with your set of data can be very useful. Use this tool to see your data set's number of possible unique combinations and repetitive combinations.

Required Information

Total Number of Objects (n):

Sample Size (r):

Result:

What it is

What are Combinations?

Create Date: September 25, 2024

Last Modified Date: December 19, 2024

Combinations refer to the grouping of items. These groupings may or may not allow repetition. For example, you have 4 objects: A, B, C, and D. If repetition is not allowed, there is only 1 unique combination (ABCD). With repetition allowed, there are 35 possible combinations (ABCD, ABDC, ADBC, DABC, etc.).

How to Calculate Combinations

Calculating how many unique combinations you can make out of a set of data can be done with the following variables:

Total number of options

Sample size to choose from them

Then you can use the following formula to find the number of combinations:

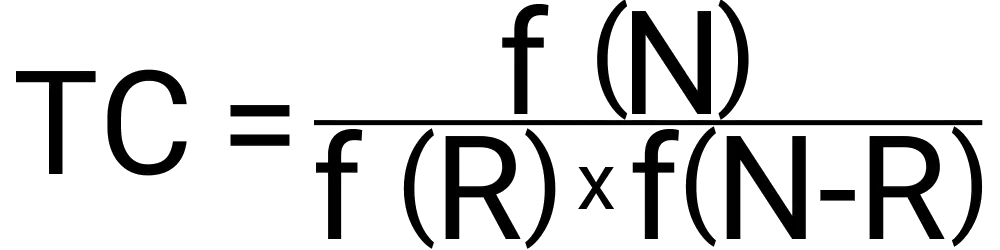
An image of the formula used to calculate how many combinations you can make with a certain number of options and how many you want to choose from them.

Where:

TC = Total combinations

f = Factorial

N = Total number of options

R = Total number of options chosen

Understanding Your Results

When you use this tool, you will get two results. You will first see the number of unique combinations that can be made. This number is how many times your chosen set of options can be picked without any type of repetition or position-based shifting. If you have 5 options: A, B, C, D, E and want to choose 5 of them you would have only 1 unique combination. This is because you are choosing all 5 options and no matter what can not shift their positions to make new ones. If you choose only 4 of those 5 you can then make 5 unique combinations. You will also be shown your total number of combinations which does allow for position shifting to count as a new combination. If we use the same example as above, the total number of combinations you would have is 126.

How to Use the Combinations Tool

Calculating how many combinations, both unique or not, you can create from a set of options can be done with ease with this tool. What is typically a hard number to calculate can be done within seconds with this tool. The steps involved with using this tool include:

Enter the total number of objects that could possibly be picked.

Enter the sample size, or the number of objects that you want to pick from the total set of objects.

Hit the calculate button and instantly get your results.

Calculation Example

We have a set of data that we want to analyze further in terms of the possible combinations we can make with it. We can use this tool to help us with that. The total number of objects or options that we have is 8. We want to use 6 of those objects as our sample size and find out how many combinations we can get. We will enter 8 into the first field then enter 6 into the second field. We can now hit calculate and learn that we can make 28 unique combinations or a total of 1,716 non-unique combinations.

Combinations - Frequently Asked Questions

A combination does not consider the order of items, while a permutation does. For example, the combination of {A, B} is the same as {B, A}, but they are two different permutations.

Use combinations when the order of items does not matter. Use permutations when the order does matter.

No, combinations always result in whole, non-negative numbers because they represent the count of possible groupings.

Combinations are often referred to as binomial coefficients. They represent the coefficients of terms in the expansion of (x + y)ⁿ.

Similar Tools

Related Calculators

We have many more calculators that you can use for free. Here are a few similar tools that might interest you.