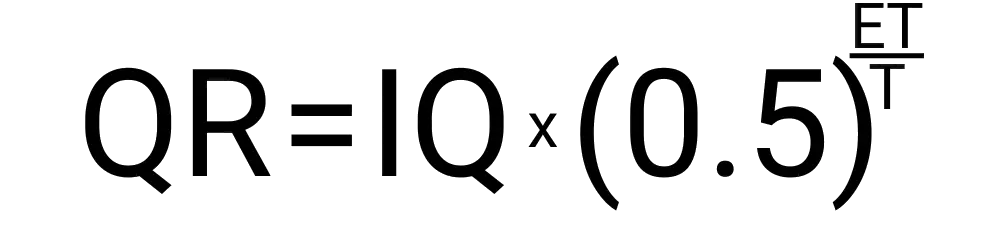Remaining Quantity:
Decay Constant:
Mean Lifetime:
Create Date: October 16, 2024
Last Modified Date: February 12, 2025
Calculating the half-life of a substance can be done with the following variables:
When you use this tool you will get three different results. First, you will see the remaining quantity of the substance based on your specified situation. Then, you will see the decay constant. This is the rate at which the substance is decaying at based on the unit of measurement selected. By default, this is shown as per second but can be changed to many other intervals. Finally, you will get your mean lifetime. This refers to the average time it takes for particles in a radioactive sample to decay. It is a statistical measure that provides insight into the average duration of a particle's existence before decaying. It will always be larger than the half-life time.
This tool simplifies the process of determining the remaining quantity of a substance after a specified time. To use it:
For example, if a substance starts with a quantity of 100 units, has a half-life of 2 hours, and 6 hours have elapsed, the remaining quantity can be calculated as follows:
The concept of half-life is not one that goes back thousands of years. Some of the earliest roots for half-life can be traced back to 1896 when Henri Becquerel discovered that uranium salts emitted radiation without external energy input, making it the first observation of radioactive decay.
Just a couple of years later, in 1898, Marie and Pierre Curie made the discovery of polonium and radium which would show that some elements naturally break down into other elements over time. This would begin the conversation around a new concept where elements were not eternal but could transform into other elements.
The true first steps to understanding half-life and naming its existence happened around 1900. Physicist Ernest Rutherford and chemist Frederick Soffy discovered that radioactive elements decayed into different elements at fixed rates. They would introduce the idea of an exponential decay process. It wouldn't be until 1907 when the term half-life would be created by Rutherford.
The concept has had extensive research and experimentation since then, over a century of different scientists and minds coming together to learn more about the topic. The concept also would be used in many other areas of study and experimentation and is a major piece of information today.
A half-life of 2 hours means it will take 2 hours for a substance to reduce its quantity to half of its current amount.
No, half-life cannot be negative as it represents a positive time interval.
Tellurium-128 has an exceptionally long half-life of 2.2 x 1024 years, far exceeding the age of the universe.
Understanding half-life can be difficult if some of the terms and keywords used are not ones you understand. Here we shed some more light on some of these terms.
| Term | Definition |
|---|---|
| Half-life time | This is the amount of time that it takes for a radioactive element to decay by half. |
There are many interesting things that can be shared about half-life. Here are some of our favorites.
Bananas contain potassium-40, a naturally radioactive isotope with a half-life of 1.25 billion years. But you could never eat enough bananas quick enough to be harmed by radiation.
The half-life of Uranium-238 is 4.5 billion years—about the same age as Earth. Scientists use this long half-life to date ancient rocks and determine Earth’s age!
The isotope Hydrogen-7 has a half-life of just 23 yoctoseconds (0.000000000000000000000023 seconds)! It decays almost instantly after being formed.
