Create Date: July 3, 2024
Last Modified Date: January 15, 2025
Calculating slope can be done when you have two different points. You will need the coordinates, once you have those you can use the following formula to find the slope:
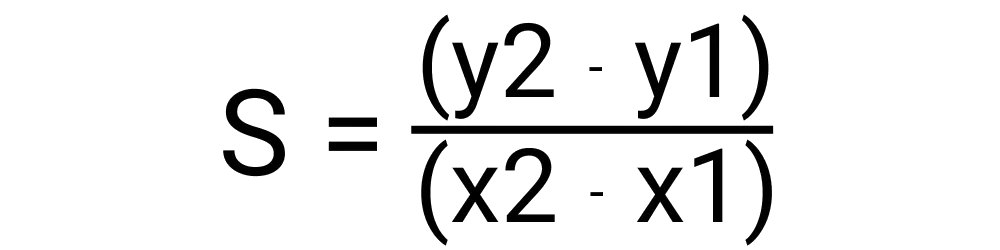
Your result will be a single number. This number represents the slops of the line that you outline with your entries. The slop of a line can be negative at times depending on the specific points in question.
Using our tool to help you find the slope of a line is very easy and efficient. We made our tool handle all the math so you can simply get your answer. The steps involved with using our tool include:
Lets say we need to calculate the slope of a line for our math homework. We can use our tool to help us do that. We have two points: (4, 5) and (5, 8). To use this tool to get the slope we will have to enter these values into the tool. So we will first enter 4 and 5 into x1 and y1, then we will enter 5 and 8 in x2 and y2.
We can now hit calculate and get our slope. We find that the slope is equal to 3.
The slope of a line represents its steepness and direction. Mathematically, it is the ratio of the vertical change (rise) to the horizontal change (run) between two points on the line. A positive slope means the line ascends from left to right, while a negative slope indicates it descends.
Yes, a slope of zero indicates that the line is perfectly horizontal. This means there is no vertical change between the two points, despite the horizontal distance.
An undefined slope occurs when a line is vertical, meaning there is no horizontal change between the two points (the denominator in the slope formula becomes zero). This is typically represented by a division by zero in mathematical terms.
Common mistakes include not accurately identifying the coordinates of the points, especially on a graph, and mixing up the order of subtraction which can lead to a sign error in the slope. Always ensure that the coordinates are accurately noted and the formula is applied correctly.