Create Date: June 16, 2024
Last Modified Date: January 14, 2025
Calculating the circumference of a circle requires only a single variable: its radius. With that known, you can use it in the following formula to calculate its circumference:
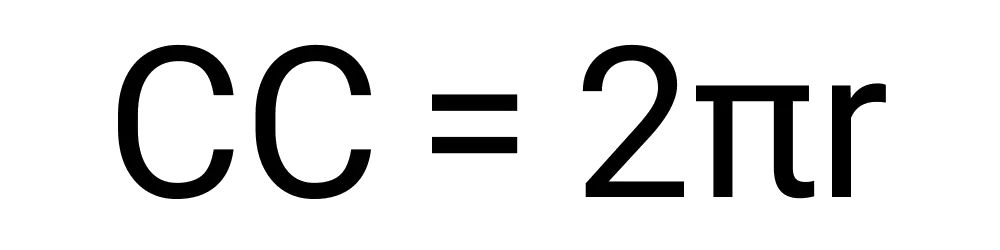
Your answer will be a single number that would signify the circumference of a circle. The circumference is the entire perimeter of a circle. This tool does not have any units of measurement on it so when you are using it you will need to add your own when you get your answer to fit your current situation.
If you are trying to find the circumference of a circle this is the tool for you. It is designed to be as easy and simple as possible. The steps required to use it include:
Let's say we have a circle that has a radius of 5. If we need to find the circumference of it we can easily do so with this tool. All we need to do is enter 5 into the singular field on this tool then hit calculate. We come to find that our circle's circumference is 31.42.
Knowing the circumference of a circle is useful in various real-world applications, including:
Yes, the circumference can be a whole number, but this depends on the radius or diameter and their relation to π. Because π is an irrational number, the circumference is often not a whole number when calculated with exact values of π.